慣性モーメント
平行軸の定理の検証
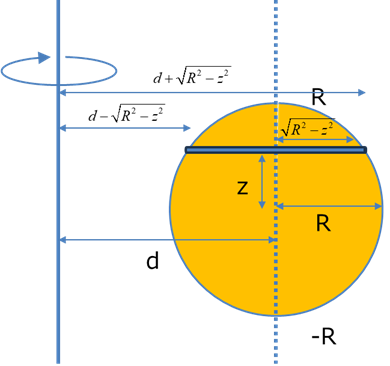
円板の場合
・円板の場合(団扇)

棒の慣性モーメントの求め方が基本となりますが,長さがzによって変化します.
したがって,まずは棒の積分を行い,次にz方向に積分していきます.
\( \Large \displaystyle J_{disk-03} = \int_{-R}^{R} dz \ \int_{d- \sqrt{R^2 - z^2}}^{d+ \sqrt{R^2 - z^2}} x^2 \rho \ dx \)
最初の積分は,
\( \Large \displaystyle \int_{d- \sqrt{R^2 - z^2}}^{d+ \sqrt{R^2 - z^2}} x^2 \rho \ dx
= \rho \left[ \frac{1}{3} x^3 \right]_{d- \sqrt{R^2 - z^2}}^{d+ \sqrt{R^2 - z^2}}
\)
\( \Large \displaystyle =\frac{1}{3} \rho \left[ (d+ \sqrt{R^2 - z^2})^3 -(d- \sqrt{R^2 - z^2})^3 \right] \)
ここで,
\( \Large \displaystyle
(d+a)^3 - (d-a)^3 = (d^3 + 3da^2 + 3d^2a+a^3) -
(d^3 + 3da^2 - 3d^2a-a^3)
= 6d^2a + 2a^3
\)
となるので,
\( \Large \displaystyle
\frac{1}{3} \rho \left[ (d+ \sqrt{R^2 - z^2})^3 -(d- \sqrt{R^2 - z^2})^3 \right]
= \frac{1}{3} \rho \left[ 6d^2 \sqrt{R^2 - z^2} + 2( R^2 - z^2)^{3/2} \right]
\)
となります.したがって
\( \Large \displaystyle J_{disk-03} = \int_{-R}^{R} \frac{1}{3} \rho \left[ 6d^2 \sqrt{R^2 - z^2} + 2( R^2 - z^2)^{3/2} \right] \ dz \)
を計算すればいいことになります.ここで,各項について検討していきます.
・1/2乗
\( \Large \displaystyle \int_{-R}^{R} \sqrt{R^2 - z^2} \ dz \)
変数変換して,
\( \Large \displaystyle z = R \ sin \theta \)
\( \Large \displaystyle dz = R \ cos \theta \ d \theta \)
\( \Large \displaystyle 0 \sim z \sim R \)
\( \Large \displaystyle 0 \sim \theta \sim \frac{ \pi}{2} \)
\( \Large \displaystyle \int_{-R}^{R} \sqrt{R^2 - z^2} \ dz = 2 \int_{0}^{\pi/2} \sqrt{R^2 - R^2 \ sin^2 \theta} \cdot R \ cos \theta \ d \theta \)
\( \Large \displaystyle = 2 \int_{0}^{\pi/2} R \ cos \theta \cdot R \ cos \theta \ d \theta \)
\( \Large \displaystyle = 2 \int_{0}^{\pi/2} R^2 \ cos^2 \theta \ d \theta \)
\( \Large \displaystyle = R^2 \int_{0}^{\pi/2} ( 1 + \ cos \ 2 \theta) \ d \theta \)
\( \Large \displaystyle = R^2 \int_{0}^{\pi/2} ( 1 + \ cos \ 2 \theta) \ d \theta \)
\( \Large \displaystyle = R^2 \left[ \theta + \frac{1}{2} sin \ 2 \theta \right]_0^{\pi/2} \)
\( \Large \displaystyle = R^2 \frac{\pi}{2} \)
・3/2乗
\( \Large \displaystyle \int_{-R}^{R} \ ( R^2 - z^2)^{3/2} \ dz \)
3/2乗に関しては,こちら,でも説明していますが,もう一度.
変数変換して,
\( \Large \displaystyle z = R \ sin \theta \)
\( \Large \displaystyle dz = R \ cos \theta \ d \theta \)
\( \Large \displaystyle 0 \sim z \sim R \)
\( \Large \displaystyle 0 \sim \theta \sim \frac{ \pi}{2} \)
\( \Large \displaystyle 2 \int_{0 }^{R }
(R^2 - z^2)^{3/2} dz
= 2 \int_{0 }^{\frac{ \pi}{2} }
(R^2 - R^2 \ sin^2 \theta )^{3/2} \cdot R \ cos \theta d \theta \)
\( \Large \displaystyle =2 \int_{0 }^{\frac{ \pi}{2} } (R^2 \ cos^2 \theta )^{3/2} R \ cos \theta d \theta \)
\( \Large \displaystyle = 2 R^4 \int_{0 }^{\frac{ \pi}{2} } cos^4 \theta \ d \theta \)
この積分は,ここ,にあるような公式を使って,
\( \Large \displaystyle
\int_{0 }^{\frac{ \pi}{2} }
cos^4 \theta \ d \theta =
\int_{0 }^{\frac{ \pi}{2} }
\frac{ 3 + 4 \ cos \ 2 \theta + cos \ 4 \theta}{8} d \theta \)
第二項,第三項は,θがπ,2πとなり,cos関数は0となります.したがって,
\( \Large \displaystyle
2 R^4 \int_{0 }^{\frac{ \pi}{2} }
cos^4 \theta \ d \theta =
2 R^4 \int_{0 }^{\frac{ \pi}{2} }
\frac{ 3 }{8} d \theta
= 2 R^4 \frac{ 3 }{8} \displaystyle
\left[ \theta \right]_0^{\frac{ \pi}{2}}
=
\frac{ 3 \pi}{8} R^4 \)
したがって,
\( \Large \displaystyle J_{disk-03} = \int_{-R}^{R} \frac{1}{3} \rho \left[ 6d^2 \sqrt{R^2 - z^2} + 2( R^2 - z^2)^{3/2} \right] \ dz \)
\( \Large \displaystyle = \rho \left[ 2 d^2 \cdot R^2 \frac{\pi}{2} + 2 \cdot \frac{1}{3} \frac{ 3 \pi}{8} R^4 \right] \)
\( \Large \displaystyle = \rho \left[ \pi R^2 d^2 + \frac{ \pi }{4} R^4 \right] \)
面密度は,半径Rの場合,
\( \Large \displaystyle M = \pi R^2 \rho \)
となるので,
\( \Large \displaystyle J_{disk-2} = \frac{M}{ \pi R^2} \left[ \pi R^2 d^2 + \frac{ \pi }{4}
R^4 \right]
= \boldsymbol{ Md^2 + \frac{1}{4}MR^2}
\)
となり,第一項が平行軸の定理,第二項が円板(団扇)の慣性モーメントとなり,平行軸の定理と一致します.
次ページは,円板(水平)の平行軸の定理の検証,を検討していきます.